Table of Contents
ScaLAPACK
Parallel Linear Algebra with ScaLAPACK
ScaLAPACK is a library of high-performance linear algebra routines for parallel distributed memory machines. On GWDG's scientific computing cluster ScaLAPACK is available from the Intel® Math Kernel Library, currently installed in version 11.1. ScaLAPACK provides often used algorithms for dense and banded matrices: the solution of systems of equations, of east squares problems, eigenvalue problems, and singular value problems.
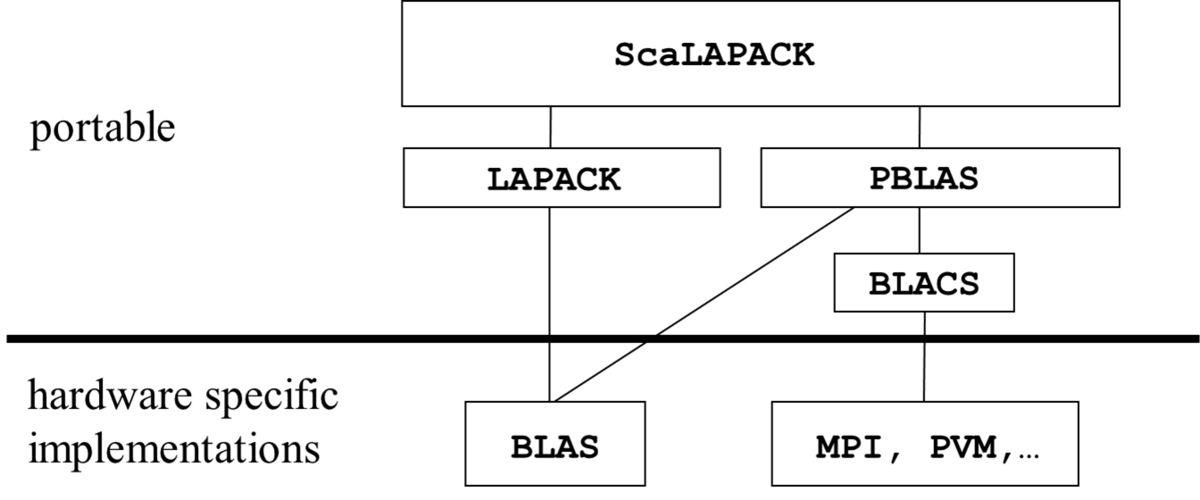
The distributed memory parallelisme of ScaLAPACK is based on the Basic Linear Algebra Communication Subprograms (BLACS) supporting the 2-dimensional data- and process-patterns used in ScaLAPACK for the efficient parallelization of the matrix algorithms of linear algebra. The BLACS are built on top of a message passing library, which is MPI for the Intel MKL implementation of BLACS. The parallel basic matrix operations used in ScaLAPACK are provided by the Parallel Basic Linear Algebra Subprograms (PBLAS), which in turn at the single process level call the Basic Linear Algebra Subprograms (BLAS) for matrix computations. This software hierarchy of ScaLAPACK is displayed in the following figure:
The performance of the ScaLAPACK routines depends on the performance of the underlying implementations of BLAS and the message passing library. With Intel MPI and Intel MKL optimal performance will be achieved on GWDG's clusters.
Documentation for ScaLAPACK and related software can be obtained from the web: ScaLAPACK, PBLAS, LAPACK, BLAS, BLACS, MPI. Furthermore the reference manual for Intel MKL gives detailed descriptions for all routines.
Speed up from parallel computing for linear algebra algorithms can easily be realized by the ScaLAPACK procedures. But even for users familiar with parallel applications based on MPI the calling of ScaLAPACK procedures needs some explanation. This concerns the use of the additional communication interface of the BLACS and the special block-cyclically distributed data layout for matrices, which is the basis for a good load balance in the parallelized matrix multiplication and matrix factorization operations of linear algebra algorithms.
First Steps for Using ScaLAPACK on GWDG Compute Clusters
A Parallel HELLO_WORLD Program with BLACS
The following example code shows how to set up the BLACS environment needed for calling ScaLAPACK procedures:
program hello_from_BLACS
implicit none
! local variables
integer info, nproc, nprow, npcol,
: myid, myrow, mycol,
: ctxt, ctxt_sys, ctxt_all
! determine rank of calling process and the size of processor set
call BLACS_PINFO(myid,nproc)
! get the internal default context
call BLACS_GET( 0, 0, ctxt_sys )
! Set up a process grid for the process set
ctxt_all = ctxt_sys
call BLACS_GRIDINIT( ctxt_all, 'C', nproc, 1)
call BLACS_BARRIER(ctxt_all,'A')
! Set up a process grid of size 3*2
ctxt = ctxt_sys
call BLACS_GRIDINIT( ctxt, 'C', 3, 2)
! All processes not belonging to ctxt jump to the end of the program
if (ctxt.lt.0) go to 1000
! Get the process coordinates in the grid
call BLACS_GRIDINFO( ctxt, nprow, npcol, myrow, mycol )
write(6,*) 'hello from process',myid,myrow,mycol, nprow, npcol
! ...
! now ScaLAPACK or PBLAS procedures can be used
! ...
1000 continue
! return all BLACS contexts
call BLACS_EXIT(0)
stop
end
For the MPI based implementation of the BLACS, the initial call to BLACS_PINFO is equivalent to calling the MPI routines MPI_INIT, MPI_COMM_SIZE and MPI_COMM_RANK. Therefore subsequent calls to all MPI routines are possible (don't forget to include the MPI file 'mpif.h'), except to MPI_INIT, which would stop the program with the MPI error message Cannot call MPI_INIT or MPI_INIT_THREAD more than once. Calling BLACS_PINFO(myid,nproc) returns in myid the task id of the calling process and in nproc the number of processes, which have been created by starting the program with the mpirun command.
The next step is setting up a two-dimensional process grid by calling BLACS_GRIDINIT(context,order,nprow,npcol). This call maps nprow*npcol processes from the process set created by starting the program to a nprow x npcol grid. The mapping is defined by assigning to a process with linear rank myid, 0⇐ myid< nprow*npcol a unique rank tuple (myrow,mycol), 0⇐myrow<nprow, 0⇐mycol<npcol in the grid. The processes are placed in the grid column after column, if order = 'C' and row after row if order = 'R'. Processes with linear ranks myid>= nprow*npcol will be mapped to the rank tuple (-1,-1). If the number of available processes is smaller than the size of the process grid to be created, the call to BLACS_GRIDINIT will cause a program abortion.
The context parameter in the call to BLACS_GRIDINIT on input has to be a valid system context, which is retrieved by the previous call to BLACS_GET(0,0,ctxt_sys), on output it gives an integer handle to the internal representation of the grid context. The context handle is set to -1 in all processes not belonging to the grid.
As the example shows, it is possible to create different grids with their own contexts form the available processor set, such that some processes will have multiple grid coordinates, depending on the context. The first call of BLACS_GRIDINIT creates a grid of size nproc x 1 with context ctxt_all, which contains all started processes. It is convenient to have all processes belonging to at least one context, because the call to BLACS_EXIT at the end of the program, which frees all contexts and releases all memory allocated internally for using the BLACS, is effective only for processes belonging to a BLACS context.
Next a grid of size 3×2 is created with context ctxt and all processes not belonging to this context jump to the end of the program. The processes of the grid then inquire the grid size and their ranks by calling the BLACS_GRIDINFO routine and write this information to the standard output device.
Compiling and Running the Program on GWDG Compute Clusters
In order to compile this program for running on the GWDG compute cluster, the necessary modules for using Intels compiler, MPI and MKL must be loaded by the command
module load intel/compiler intel-mpi intel/mkl
The compilation then must include linking the needed libraries, as described in the Intel MKL User's Guide. An example for using the sequential MKL library (one thread per process) is
mpiifort -o hello hello_from_BLACS -L$(MKLROOT)/lib/intel64/
-lmkl_scalapack_lp64
-lmkl_blacs_intelmpi_lp64
-lmkl_intel_lp64
-lmkl_sequential
-lmkl_core
These libraries are also selected for linking by using the option -mkl=cluster, for example
mpiifort -o hello hello_from_BLACS -mkl=cluster
Finally, the program can be started with at least 6 processes interactively with the mpirun command, for example
mpirun -n 7 hello
producing the output
hello from process 0 0 0 3 2 hello from process 1 1 0 3 2 hello from process 2 2 0 3 2 hello from process 3 0 1 3 2 hello from process 4 1 1 3 2 hello from process 5 2 1 3 2
With the bsub command the program can submitted to the queueing system for running on the compute cluster.
bsub -q mpi-short -o out.%J -n 7 -a intelmpi mpirun.lsf ./hello
More information on using the queueing system on the GWDG comte cluster is provided on the GWDG Wiki under the header https://info.gwdg.de/docs/doku.php?id=en:services:application_services:high_performance_computing:running_jobs.
Block-Cyclic Data Distribution
In ScaLAPACK, all arrays are block-cyclically distributed over the available process grid. This distribution will be explained in detail for vector- and matrix-data in the next two sections.
Block-Cyclic Vector Distribution
The block-cyclic distribution of a vector over a linearly arranged processor set is characterized by 4 numbers
n size of vector nb size of blocks nproc size of linear processs set psrc process containing the first element of the vector
In the block-cyclic distribution of a vector the blocks are placed cyclically to the available processes in the process set, starting on process psrc. The blocks are stored contiguously in the local memory of a process. If n is not divisible by nb, the last block will contain less than nb values. The folowing figures illustrate the block-cyclic distribution for
n=9, nb=2, nproc=2, psrc=1:
In order to determine the individual sizes of local parts of the vector stored in process ip, the vector size n is split up as
n = (nblock-1)*nb + nlast,
where nblock=⌈n/nb⌉ is the total number of blocks, of which nblock-1 are of full size nb and one of size 0<nlast≤nb, the number of remaining elements of the vector.
The nblock blocks are distributed in a round-robin order to the nproc available processes:
nblock = (lblock-1)*nproc + lfirst
such that the first 0<lfirst≤nproc processes will store lblock=⌈nblock/nproc⌉ blocks, the remaining nproc-lfirst processes storing lblock-1 blocks. The last block stored in the last of the lfirst processes is of size 0<nlast≤nb, all others are of full size nb.
ScaLAPACK provides the utility function NUMROC (number of rows or columns), which implements this calculation to determine the local number of elements on process ip, given the four numbers n, nb, prsc, nproc. A demo version providing the functionaly of NUMROC is
integer function NUMROC_demo( n, nb, ip, psrc, nproc )
implicit none
integer n, nb, ip, psrc, nproc
integer nblock, nlast, lblock, lfirst, ip0
! ip0 is the distance of ip to psrc
ip0 = mod(nproc+ip-psrc,nproc)
nblock = (n+nb-1)/nb; nlast = n - (nblock-1)*nb
lblock = (nblock+nproc-1)/nproc; lfirst = nblock - (lblock-1)*nproc
if ( ip0.lt.lfirst ) then
numrock = lblock*nb
else if ( ip0.eq.lfirst ) then
numrock = (lblock-1)*nb +nlast
else
numrock = (lblock-1)*nb
end if
return
end
The maximal number of local elements in any process is given by
if (lfirst.eq.0) NUMROC ≤ (lblock-1)*nb + nlast < lblock*nb if (lrest.gt.0) NUMROC ≤ lblock*nb.
Therefore LELM=lblock*nb is an upper bound for the NUMROC function:
LELM(n,nb,nproc) = lblock*nb = nb*⌈⌈n/nb⌉/nproc⌉
= nb*⌈n/(nb*nproc)⌉ = nb*(⌊(n-1)/(nb*nproc)⌋+1);
≤ ⌊(n-1)/nproc⌋ + nb
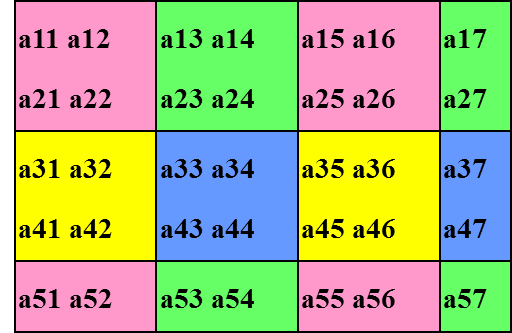
Block-Cyclic Matrix Distribution
The block-cyclic distribution of a two dimensioinal array on an two dimensional process grid is a direct product of block-cyclic distribution in each dimension. The relevant parameters for the matrix distribution are
m,n number of rows and columns of the matrix mb, nb sizes of blocks in columns and in rows nprow, npcol number of rows and columns of the two dimensional process grid rsrc, csrc row and column index of the process containing the first element of the matrix
The folowing figures illustrate the block-cyclic matrix distribution with parameters
m=5,n=7, mb=nb=2, nprow=npcol=2, rsrc=csrc=0:
Mapping between Global and Local Indices
In order to transform a global mxn matrix A to a block-cyclically distributed data set, an element A(i,j) of the global matrix must be stored as an element al(il,jl) of the local matrix al in a process with task tupel (ip,jp). This mapping i↔(il,ip) depends on block size nb of rows or columns, the number proceses np in a row or column in the process grid and on the value sp for row or column of the process grid containing the first element of the matrix. For given values of nb, np, sp, the mapping i→(il,ip) is defined by the steps
im = i-1 i1 = im modulo nb i2 = im - nb*i1 k = i1 modulo np rp = i1 - np*k ip = sp + rp modulo np il = k*nb + i2 + 1
and the reverse mapping i←(il,ip) by
rp = ip - sp + np modulo np ilm = il-1 k = ilm modulo nb i2 = ilm - nb*k i1 = k*np + rp i = i1*nb + i2+1
These mappings are provided by ScaLAPACK tool functions
i = INDXL2G(il,nb,ip,sp,np) il = INDXG2L(i,nb,id1,id2,np) ip = INDXG2P(i,np,id1,sp,np)
where id1,id2 in INDXG2L and id1 in INDXG2P are dummy integer variables, included to unify the calling sequences of these functions.
Supposing, that the values for the element A(i,j) of the global mxn matrix is given by the function matval(i,j) the mapping function can be used to place these values sequentially to their storage locations in the local arrays al, as shown in the following code fragment. The leading dimension for the local matrix in this code is given by llda = max(1,NUMROC( m, mb, myrow, 0, nprow )) and the source process containing the first element A(1,1) is assumed to be (0,0).
! copy the values of the global matrix
! to the local parts of the distributed matrix
llda = max(1,NUMROC( m, mb, myrow, 0, nprow ))
do j = 1 , n
jl = INDXG2L(j,nb,0,0,npcol)
ipc = INDXG2P(j,nb,0,0,npcol)
do i = 1 , m
il = INDXG2L(i,mb,0,0,nprow)
ipr = INDXG2P(i,mb,0,0,nprow)
if (ipr.eq.myrow.and.ipc.eq.mycol)
: al(il+llda*(jl-1))= matval(i,j)
end do
end do
Alternatively, the local parts al of the distributed matrix can be initialized in parallel using the inverse mapping
! initialize in parallel the local parts of the distributed matrix
mll = NUMROC( m, mb, myrow, 0, nprow )
nll = NUMROC( n, nb, mycol, 0, npcol )
do jl = 1 , nll
j = INDXL2G(jl,nb,mycol,0,npcol)
do il = 1 , mll
i = INDXL2G(il,mb,myrow,0,nprow)
al(il+mll*(jl-1))= matval(i,j)
end do
end do
A complete example program for using these mapping routines for initializing the distributed matrix can be copied from here.
Array Descriptors in ScaLAPACK
In ScaLAPACK the information about the block-cyclic data distribution for an array is encoded in an integer vector with 9 elements, called descriptor. Let desc_A denote the descriptor for the array A. It's elements have the following meaning:
desc_A(1) = 1 only possible value for the descriptor type desc_A(2) = ctxt_A BLACS context for the distribution of the global matrix A desc_A(3) = m_A number of rows of global matrix A desc_A(4) = n_A number of columns of global matrix A desc_A(5) = mb_A column block size for the distribution of A desc_A(6) = nb_A row block size for the distribution of A desc_A(7) = rsrc_A process row in the ctxt_A grid containing the first row of A desc_A(8) = csrc_A process column in the ctxt_A grid containing the first column of A desc_A(9) = llda leading dimension of the local matrix containing elements of A
The first 8 elements of the descriptor describe global properties of the distributed matrix, they must be equal for all participating processes in the grid context ctxt_A. Only the 9th element describes a local property of the distribution. llda must be greater or equal than NUMROC( m_A, mb_A, myrow, rsrc_A , nprow ), the number of rows of the global matrix assigned to the calling process. Although there are no descriptor elements containing the sizes of the grid dimensions, this information is available from the descriptor indirectly via the element containing the context handle.
All calls to ScaLAPACK and PBLAS routines involve the descriptors for the distributed matrices participating in operations performed by the subroutines. The descriptors have to be initialized accordingly before calling the routines. The initialization can be done explicitely by assigning the appropriate values to the descriptor elements or by calling the special initialization routine DESCINIT. The calling sequence for DESCINIT is:
call DESCINIT( desc_A, m_A, n_A, mb_A, nb_A, rsrc_A, csrc_A, ctxt_A, llda, info )
Attention must be payed to the order of parameters in the calling sequence, which does not follow completely the numbering order of these values in the descriptor array.
If the descriptor desc_A was initialized successfully, the integer output paramter info returns 0,. Otherwise, if parameter number pos is the first to have an illegal value, the return value of info is -pos and in addition an error message will be produced.
The Matrix Redistribution Routine PDGEMR2D
A further possibility to initialize the local parts of a distributed matrix is provided within ScaLAPACK by the matrix redistribution subroutine PDGEMR2D. This routine copies a submatrix from a given block-cyclically distributed global matrix A, characterized by a grid context ctxt_A and a matrix descriptor desc_A to a submatrix of the same size of another block-cyclically distributed global matrix B characterized by ctxt_B and desc_B. The two matrices A and B can have different sizes, block-sizes and can be distributed on different sized process grids defined in the set of participating processes. Of course the sizes of A and B must be large enough to contain the submatrices to be used as input and output for the copy operation.
The calling sequence for the general case is
call PDGEMR2D(m, n, al, i_A, j_A, desc_A, bl, i_B, j_B, desc_B, ctxt)
m, n number of rows and columns of the submatrix to be copied
al local matrix of size llda * nla, llda = desc_A(9),
nla is the number of columns of the global submatrix of A stored in the process,
equal to NUMROC( n_A, nb_A, mycol, csrc_A , npcol )
on input, al must contain the local elements of the submatrix of the global matrix A
i_A, j_A indices in the global matrix A, where the submatrix to be copied starts
desc_A descriptor of global matrix A
for processes not belonging to ctxt_A:
desc_A(2) must be set to -1, other values of desc_A are ignored
bl local matrix of size lldb * nlb, lldb = desc_B(9),
nlb is the number of columns of the global submatrix of B stored in the process,
equal to NUMROC( n_B, nb_B, mycol, csrc_B , npcol )
on output, bl will contain the local elements of the submatrix of the global matrix B
i_B, j_B indices in the global matrix B, where the submatrix to be stored starts
desc_B descriptor of global matrix B
for processes not belonging to ctxt_B:
desc_B(2) must be set to -1, other values of desc_B are ignored
ctxt valid context handel pointing to a process grid,
which contains all processes used in ctxt_A and ctxt_B
For generating a block-cyclically distributed copy of a global matrix A, the global matrix is generated as an ordinary two-dimensional local array a_0 on process 0, which then is copied using PDGEMR2D to the local arrays al in the processes of the two dimensional process grid. The following lines of code illustrate this:
call BLACS_PINFO(myid,nproc)
call BLACS_GET( 0, 0, ctxt_sys )
! Set up a process grid of size 3*2 with context ctxt
ctxt = ctxt_sys
call BLACS_GRIDINIT( ctxt, 'R', 3, 2)
! Set up a process grid of size 1 with context ctxt_0
ctxt_0 = ctxt_sys
call BLACS_GRIDINIT( ctxt_0, 'R', 1, 1)
! Get the process coordinates in the grid context ctxt
call BLACS_GRIDINFO( ctxt, nprow, npcol, myrow, mycol )
! initialize the descriptor for the distributed mxn matrix:
llda = max(1,NUMROC( m, mb, myrow, 0, nprow ))
call DESCINIT( desca, m, n, mb, nb, 0, 0, ctxt, llda, info )
! initialize the descriptor desca_0 for the global mxn matrix:
desca_0(2) = -1
if (myid.eq.0)
: call DESCINIT( desca_0, m, n, m, n, 0, 0, ctxt_0, m,info )
! on proc 0 initialize the global matrix a_0
if (myid.eq.0) then
do j = 1, n
do i = 1 , m
a_0(i + m * (j - 1)) = matval(i,j)
end do
end do
end if
! copy a_0 on process 0 block-cyclically to the local arrays al in the process grid
call PDGEMR2D(m, n, a_0, 1, 1, desca_0, al, 1, 1, desca, ctxt)
A complete example program for using PDGEMR2D can be copied from here.
Example Programs with PBLAS Routines
PBLAS provides basic linear algebra operations on vectors and matrices for parallel execution in a message passing programming environment. A matrix operand in PBLAS is a submatrix sub(A) with m rows and n columns of a global matrix A with m_A rows and n_A columns, which starts at the element of A with rowindex i_A and column_index j_A.
sub(A)(1:m,1:n) = A(i_A:i_A+m-1,j_A:j_A+n-1)
For a valid submatrix the following restrictions have to be met:
1<=i_A<=m_A, 1<=j_A<=n_A, i_A+m-1<=m_A, j_A+n-1 <=n_A
The local array al of a matrix operand in a call to a PBLAS routine is assumed to contain the elements of the global matrix A, which are mapped to the calling process according to the parameters in the descriptor desc_A describing the block-cyclic distribution of A in the given process grid. This mapping is independent of i_A and j_A defining the location of the global submatrix sub(A) within the global matrix A. Therefore the leading dimension for the local array al, which has to be provided as desc_A(9) in the array descriptor for matrix A has to be larger or equal to NUMROC( m_A, mb_A, myrow, rsrc, nprow ), independent of the number of rows m of sub(A) and of the location i_A of the first row of sub(A) within the global Matrix A. The number of columns in the local array al actually needed for the operation with the operand sub(A) is NUMROC(j_A+n-1, nb_A, mycol, csrc, npcol ) and thus depends on the size and location of sub(A).
A vector operand in PBLAS is a special submatrix of a global matrix X with only one column or one row:
subcol(X)(1:m) = X(i_X,i_X+m-1,j_X:j_X) subrow(X)(1:n) = X(i_X:i_X,j_X:j_X+n-1)
Parallel Matrix Vector Multiplication with PDGEMV
The parallel matrix vector multiplication provided by the PBLAS routine PDGEMV works with three global matrices A, X, Y, which are distributed according to descriptors desc_A, desc_X, desc_Y. PDGEMV performs the operation
subvec(Y) = alpha sub(A) subvec(X) + beta subvec(Y)
where alpha and beta are scalars, sub(A) is a submatrix of A, subvec(X),subvec(Y) are single subrows or subcolumns of X and Y. The detailed specification of the submatrices is dictated by the parameters trans,m,n,incx,incy in the calling sequence for PDGEMV.
For trans='N'>
sub(A)(1:m,1:n) = A(i_A:i_A+m-1,j_A:j_A+n-1) if (incx=1) subcol(X)(1:n) = X(i_X:i_X+n-1,j_X:j_X) if (incx=m_X) subrow(X)(1:n) = X(i_X:i_X,j_X:j_X+n-1) if (incy=1) subcol(Y)(1:m) = Y(i_Y:i_Y+m-1,j_Y:j_Y) if (incy=m_Y) subrow(Y)(1:m) = Y(i_Y:i_Y,j_Y:j_Y+m-1)
For trans='T'>
sub(A)(1:n,1:m) = transpose of A(i_A:i_A+m-1,j_A:j_A+n-1) if (incx=1) subcol(X)(1:m) = X(i_X:i_X+m-1,j_X:j_X) if (incx=m_X) subrow(X)(1:m) = X(i_X:i_X,j_X:j_X+m-1) if (incy=1) subcol(Y)(1:n) = Y(i_Y:i_Y+n-1,j_Y:j_Y) if (incy=m_Y) subrow(Y)(1:n) = Y(i_Y:i_Y,j_Y:j_Y+n-1)
The calling sequence for PDGEMV is
call PDGEMV(trans, m, n, : alpha, al, i_A, j_A, desc_A, : xl, i_X, j_X, desc_X, incx : beta, yl, i_Y, j_Y, desc_Y, incy )
The arguments have the following meaning:
trans:
if trans = 'N' the submatrix is taken directly from A
if trans = 'T' the submatrix is taken from the transposed of A
m :
if trans = 'N', number of rows in sub(A), number of elements in subvec(Y)
if trans = 'T', number of columns in sub(A), number of elements in subvec(X)
n :
if trans = 'N', number of columns in sub(A), number of elements in subvec(X)
if trans = 'T', number of rows in sub(A), number of elements in subvec(Y)
alpha:
scalar of type real*8 multiplying sub(A)
al:
local array containing the local values of A
i_A, j_A:
row and column number in A, where the submatrix sub(A) starts
desc_A:
descriptor for the distribution of A
xl:
local array containing the local values of X
i_X, j_X:
row and column number in X where the subvector subvec(X) starts
desc_X:
descriptor for the distribution of X
incx:
if incx=1: subvec(X) is a subcolumn of X
if incx=m_X: subvec(X) is a subrow of X
beta:
scalar of type real*8 multiplying subvec(Y)
yl:
local array containing the local values of Y
i_Y, j_Y:
row and column number in Y where the subvector subvec(Y) starts
desc_Y:
descriptor for the distribution of Y
incy:
if incy=1: subvec(Y) is a subcolumn of Y
if incy=m_Y: subvec(Y) is a subrow of Y
An example code for executing a matrix vector multiplication using PDGEMV with general values for sizes and distributions of global matrices and sizes and location of submatrices can be found here. Of course the parameters for sizes of the matrices and the positions of submatrices within the matrices have to be consistent (submatrix_restrictions), otherwise the program will abort with an error message.
In the simplest case of the multiplication of an m x n matrix by an n vector yielding an m vector, the global matrix A has size m x n, the global matrix X has size n x 1, the global matrix Y has size m x 1, the respective blocksizes are chosen as mb x nb, nb x 1, mb x 1 for A, X, Y resp. and the root process for all three global matrices A, X and Y has grid coordinates (0,0). The parameters for the sizes and distributions of global matrices and sizes and locations of submatrices in this case are:
m_A = m, n_A = n, mb_A = mb, nb_A = nb, i_A = 1, j_A = 1 m_X = n, n_X = 1, mb_X = nb, nb_X = 1 , i_X = 1, j_X = 1 m_Y = m, n_Y = 1, mb_Y = mb, nb_Y = 1 , i_Y = 1, j_Y = 1 incx = 1, incy = 1, rsrc = 0, csrc = 0
On a column major process grid of size nprow x npcol the matrix A will be distributed block-cyclically over all processes of the grid, whereas X and Y will be distributed over the processes of the first column in the grid with blocksizes nb resp. mb. The relevant parts of a code for this case are
! Parameters for distributed global matrices A, X, Y
m = 69; n = 77; mb=12; nb = 13
! Parameters for processor grid
nprow=2; npcol=3
! set data for A and X; A(i,j) = mati*i + matj*j, X(i,1) = veci*i+vecj
mati = 1; matj = 1; veci=1; vecj = 1
! Set up a process grid of size nprow*npcol
ctxt = ctxt_sys; CALL BLACS_GRIDINIT( ctxt, 'C', nprow, npcol)
! Get the process coordinates in the grid
CALL BLACS_GRIDINFO( ctxt, nprow, npcol, myrow, mycol )
! number of rows and columns of local parts al, xl, yl for A, X, Y
m_al = NUMROC( m, mb, myrow, 0, nprow )
n_al = NUMROC( n, nb, mycol, 0, npcol )
m_xl = NUMROC( n, nb, myrow, 0, nprow ); n_xl = 1
m_yl = m_al; n_yl = 1
! initializing descriptors for the distributed matrices A, X, Y:
llda = max(1,m_al); lldx = max(1,m_xl); lldy = max(1,m_yl)
call DESCINIT( desc_A, m, n, mb, nb, 0, 0, ctxt, llda, info )
call DESCINIT( desc_X, n, 1, nb, 1, 0, 0, ctxt, lldx, info )
call DESCINIT( desc_Y, m, 1, mb, 1, 0, 0, ctxt, lldy, info )
! initialize in parallel the local parts al of A
do jl = 1 , n_al
call ind_lc_gl(nb,npcol,0,jl,mycol,j)
do il = 1 , m_al
call ind_lc_gl(mb,nprow,0,il,myrow,i)
al(il+m_al*(jl-1))= mati*i+matj*j
end do
end do
! initialize in parallel the local parts xl of X
do il = 1 , m_xl
call ind_lc_gl(nb,nprow,0,il,myrow,i)
xl(il)= veci*i+vecj
end do
! calculate matrix vector product
call PDGEMV( 'N', m, n,
: 1.d0, al, 1, 1, desc_A,
: xl, 1, 1, desc_X, 1,
: 0.d0, yl, 1, 1, desc_Y, 1 )
The complete program for the use of PDGEMV with this simplest case is here.
Example Programs with ScaLAPACK Driver Routines
Parallel Equation Solution with PDGESV
The ScaLAPACK driver routine PDGESV is a parallel solver of systems of linear equations
a x = b
where a is the coefficient matrix of size n x n, b is a given right hand side vector of size n and x is the vector of size n which solves this system of equations.
Similar to the PBLAS routines, PDGESV works with global block-cyclically distributed matrices, A and B, and their descriptors desc_A and desc_B. As input matrix a with the equation coefficients a submatrix sub(A) af A is used
sub(A)(1:n,1:n) = A(i_A:i_A+n-1,j_A:j_A+n-1)
and several (nrhs) right hand side vectors are given as a submatrix sub(B) of B
sub(B)(1:n,1:nrhs) = B(i_B:i_B+n-1,j_B:j_B+nrhs-1)
The nrhs solutions of these equations are stored in sub(B), overwriting the input of the right hand sides.
A pivot vector indicating the exchange of rows in the solution process is stored as a subvector of size n of a global block-cyclically distributed vector V of size m_A and block siza mb_A:
subvec(V)(1:n) = V(i_A:i_A+n-1)
The calling sequence for PDGESV is
call PDGESV (n, nrhs,
: al, i_A, j_A, desc_A, ipvtl,
: bl, i_B, j_B, desc_B, info)
The arguments have the following meaning:
n:
number of columns and rows of the global coefficient matrix sub(A)
and number of rows of the global matrix of right hand sides sub(B)
nrhs:
number of right hand sides, ie. number of columns in the global matrix sub(B)
al:
local array containing the local values of A
i_A, j_A:
row and column number in A, where the submatrix sub(A) starts
desc_A:
descriptor for the distribution of A
ipvtl:
local integer array of size llda+mb_a.
This array contains the pivoting information.
If i is the index of the global row corresponding to the local row index il
then ipvtl(il) = index of the global row which was swapped with global row i.
bl:
local array containing the local values of B,
on entry the values of bl corresponding to sub(B) contain
the local parts of the right hand sides,
on return they contain the local parts of the solution vectors
i_B, j_B:
row and column number in B where the submatrix submat(B) starts
desc_B:
descriptor for the distribution of B
info:
on return, if info=0 the coeeficient matrix sub(A) is nonsingular
if info > 0 , the coefficient matrix sub(A) is singular
and the solutions are not determined.
As in the case of the PBLAS routines PDGEMV and PDGEMM, the parameters for sizes of the matrices and the positions of submatrices within the matrices have to be consistent (submatrix_restrictions), otherwise the program will abort with an error message. For PDGESV there are further restrictions for the layout of the distributed matrices:
Blocksizes:
mb_A = nb_A
mb_B = nb_A
Positions of submatrices:
i_A-1 modulo mb_A = 0
j_A-1 modulo nb_A = 0
i_B-1 modulo mb_B = 0
the process row containing the row i_A of A
must also contain the row i_B of B
If one of these conditions is violated, the program will abort with an error message.
An example code for solving a system of equations using PDGESV with general values for sizes and distributions of global matrices and sizes and positions of submatrices can be found here.
In the simplest case the global matrix A of size nxn is the coefficient matrix and the global matrix B of size nx1 contains one right hand side on entry and the solution on return, and the root process for A and B has grid coordinates (0,0). The parameters for the sizes and distributions of global matrices and sizes and positions of submatrices in this case are:
m_A = n, n_A = n, mb_A = nb, nb_A = nb, i_A = 1, j_A = 1 m_B = n, n_B = 1, mb_B = nb, nb_B = 1 , i_B = 1, j_B = 1 rsrc_A = 0, csrc_A = 0, rsrc_B = 0, csrc_B = 0
On a column major process grid of size nprow x npcol the matrix A will be distributed block-cyclically over all processes of the grid, whereas B will be distributed over the processes of the first column in the grid with blocksizes nb. The relevant parts of a code for this case are
! Parameters for the distributed global matrices
n = 9; nb = 2
! Parameters for processor grid
nprow=2; npcol=3
! Set up a process grid of size nprow*npcol
call BLACS_GET( 0, 0, ctxt ); call BLACS_GRIDINIT( ctxt, 'C', nprow, npcol)
! Get the process coordinates in the grid
call BLACS_GRIDINFO( ctxt, nprow, npcol, myrow, mycol )
! number of rows and columns of loacal parts al, bl for A, B
m_al = NUMROC( n, nb, myrow, 0, nprow )
n_al = NUMROC( n, nb, mycol, 0, npcol )
m_bl = NUMROC( n, nb, myrow, 0, nprow )
n_bl = NUMROC( 1, 1, mycol,0, npcol )
! initializing descriptors for the distributed matrices A, B:
llda = max(1,m_al); lldb = max(1,m_bl)
call DESCINIT( desc_A, n, n, nb, nb, 0, 0, ctxt, llda, info )
call DESCINIT( desc_B, n, 1, nb, 1, 0, 0, ctxt, lldb, info )
! initialize in parallel the local parts of A in al and in al_s
do jl = 1 , n_al
j = INDXL2G(jl,nb,mycol,0,npcol)
do il = 1 , m_al
i = INDXL2G(il,nb,myrow,0,nprow)
al(il+m_al*(jl-1))= 1.d0/(1.+5.*abs(i-j))
end do
end do
! initialize in parallel the local parts of B in bl
do il = 1 , m_bl
i = INDXL2G(il,nb,myrow,0,nprow)
bl(il)= 1.*i + 1.
end do
! solve the systems of equations
call PDGESV( n, 1, al, 1, 1, desc_A, vl, bl, 1, 1, desc_B, info)
The complete program for the use of PDGESV with this simplest case is here
Parallel Eigenproblem Solution with PDSYEV
The ScaLAPACK driver routine PDSYEV determines eigenvalues λi and eigenvectors vi of a real symmetric nxn matrix a:
avi = λivi , i=1,…,n
The symmetric matrix a must be provided as a nxn submatrix sub(A) of a global block-cyclically distributed matrix A
sub(A)(1:n,1:n) = A(i_A:i_A+n-1,j_A:j_A+n-1)
the ortonormal eigenvectors vi will be returned as columns of a nxn submatrix sub(Z) of a global block-cyclically distributed matrix Z
sub(Z)(1:n,1:n) = Z(i_Z:i_Z+n-1,j_Z:j_Z+n-1)
and all n eigenvalues λi are returned in ascending order on every process in a vector w.
The complete calling sequence for PDSYEV is
call PDSYEV (jobz, uplow, n, al, i_A, j_A, desc_A, w,
: zl, i_Z, j_Z, desc_Z,
: work, lwork, info )
where the meaning of the arguments is
jobz:
if jobz = 'N', only eigenvalues are computed
if jobz = 'V', eigenvalues and eigenvectors are computed
uplo:
if uplo = 'U', the upper triangular part of the symmetric matrix sub(A) is used
if uplo = 'L', the lower triangular part of the symmetric matrix sub(A) is used
n:
order of sub(A) used in the computation
al:
local array containing the local values of A,
on return, the values of al corresponding to the upper or lower triangular part of sub(A)
are overwritten, depending on the value of uplow
i_A, j_A:
row and column number in A, where the submatrix sub(A) starts
desc_A:
descriptor for the distribution of A
w:
global array of size >=n, containing on return all n eigenvalues in ascending order
zl:
local array for the local values of Z,
containing on return the local values of the eigenvectors, if jobz = 'V'
i_Z, j_Z:
row and column number in Z where the submatrix submat(Z) starts
desc_Z:
descriptor for the distribution of Z
work:
local workspace array of size ≥ max(1,lwork)
if lwork = -1, work(1) returns the size of the needed workspace
lwork:
size of workspace reserved locally. If lwork >0 on input is less than this size,
the program aborts.
If on input globally lwork=-1, PDSYEV returns the needed workspace in work(1)
without solving the eigenproblem
info:
on return,
if info = 0, the execution is successful,
if info < 0:
if the i-th argument is an array and the j-entry had an illegal value,
then info = -(i*100+j),
if the i-th argument is a scalar and had an illegal value,
then info = -i,
if info= n+1, then PDSYEV has detected heterogeneity by finding
that eigenvalues were not identical across the process grid;
in this case, the accuracy of the results from PDSYEV cannot be guaranteed
The source code for PDSYEV includes a warning concerning the validity of its results: “In its present form, PDSYEV assumes a homogeneous system and makes no checks for consistency of the eigenvalues or eigenvectors across the different processes. Because of this, it is possible that a heterogeneous system may return incorrect results without any error messages.”
The reason for possible inconsitencies is, that some operations in PDGEMV are performed redundently in all participating processes. The parallel algorithm guaranties correctness only, if these redundant calculations give identical results on all processes. If the participating processes run on heterogeneous cpu's with different implementations for handling the rounding or overflow of floating point operations, the redundant operatioons might give different sesults, leding to inconsistecies. Since there is no complete testing for such inconsistencies, the results may be incorrect even if info=0 on return. More information on the problem of heterogeneity in parallel algorithms can be fond in this article by Blackford et al..
As in the case of the PBLAS routines PDGEMV and PDGEMM, the parameters for sizes of the matrices and the positions of submatrices within the matrices have to be consistent (submatrix_restrictions), otherwise the program will abort with an error message. For PDSYEV there are further restrictions for the layout of the distributed matrices:
Global matrices:
m_A = m_Z
n_A = n_Z
mb_A = nb_A = mb_Z = nb_Z = nb
rsrc_A = rsrc_Z
csrc_A = csrc_Z
Positions of submatrices:
i_A-1 modulo nb = 0
j_A-1 modulo nb = 0
i_Z-1 modulo nb = 0
the process row containing the row i_A of A
must also contain the row i_Z of Z
If one of these conditions is violated, the program will abort with an error message.
Furthermore, tests with PDSYEV have shown, that wrong results are produced without error message, if the offsets for the submatrices sub(A) and sub(Z) are different. This restriction is not described in the documentation contained in the source code for PDSYEV.
Each of the local processes has to provide memory space for the local parts of the global matrices A and Z and for all n eigenvalues. In addition memory space for the local workarray work is needed. The amount of memory locally allocated for work can be prescribed with the input parameter lwork. If on input lwork>0, it must be larger or equal than size_w, the workspace needed locally in a process. Two main components contribute to size_w, one is proportional to the global order n of the eigenproblem to be solved, one is proportional to the number of elements of the problem matrix stored locally.
If jobz='N' (no eigenvectors are requested)
size_w = n*5 + lel + 1
lel = workspace requirement for ScaLAPACK routine PDSYTRD
≤ nb * max(LELM(n,nb,nprow)+1,3)
where ''LELM(n,nb,nprow)=nb⌈n/(nb*nprow)⌉'' is the maximum of local elements over all processes in a column of the process grid.
For blocksizes larger than 2 therefore the following value for lwork will be sufficient on all processes:
lwork = 5n + nb( ⌊(n-1)/nprow⌋ + nb) + 1
If jobz='V' (eigenvalues and eigenvectors are requested)
size_w = n*5 + max(2*(n-2), lel1) + n*lel2 + 1
lel1 = workspace requirement for ScaLAPACK routine PDORMTR when it's SIDE argument is 'L'
≤ nb*(LELM(n+1,nb,nprow)+LELM(n+1,nb,npcol) +nb)
lel2 = number of rows of a block-cyclically (blocksize nb)
global matrix with n rows
stored locally in a process of a process grid of size (nprow*npcol) * 1
≤ LELM(n,nb,nprow*npcol)
A sufficient large value for lwork in this case is (using A = ⌊n/(nb*nprow)⌋+⌊n/(nb*npcol)⌋)
lwork = 5n + max(2n,(3+A)nb²) +nb(⌊(n-1)/(nb*nprow*npcol)⌋+1)n + 1
An example code for the determination of eigenvalues and eigenvectors using PDSYEV can be found here.
A demo code for simple values for all parameters is here. The relevant patrs for this code are
! input parameters
n = 1000; nb = 24
! Parameters for processor grid
nprow=2; npcol=2
! Set up a process grid of size nprow*npcol
call BLACS_GET( 0, 0, ctxt ); call BLACS_GRIDINIT( ctxt, 'C', nprow, npcol)
! Get the process coordinates in the grid
call BLACS_GRIDINFO( ctxt, nprow, npcol, myrow, mycol )
! number of rows and columns of local parts al, zl for A, Z
m_al = NUMROC( n, nb, myrow, 0, nprow )
n_al = NUMROC( n, nb, mycol, 0, npcol )
! size of workarray
lel1 = nb**2*(n/(nb*nprow)+n/(nb*npcol)+3)
lel2 = nb*((n-1)/(nb*nprow*npcol)+1)
lwork = n*5 + max(2*n,lel1) + n*lel2 + 1
! initializing descriptors for the distributed matrices:
llda = max(1,m_al)
call DESCINIT( desc_A, n, n, nb, nb,
: 0, 0, ctxt, llda, info )
! initialize in parallel the local parts of A in al
do jl = 1 , n_al
j = INDXL2G(jl,nb,mycol,0,npcol)
do il = 1 , m_al
i = INDXL2G(il,nb,myrow,0,nprow)
al(il+m_al*(jl-1))= 1./(1.+5.*abs(i-j))
end do
end do
! calculate eigenvalues and eigenvectors
call PDSYEV( 'V', 'U', n, al, 1, 1, desc_A, w,
: zl, 1, 1, desc_A,
: work, lwork, info )